Australia Lesson Activities - Maths

Check out the latest statistics from the Datasheet

Missions and Math

How much water do you use in a day? Think about your showers, drinking, food preparation, and even what your dog drinks! Can you imagine getting all the water you would need for six months?! That’s a lot of water!

The missionaries out here in the centre of Australia would have to get all the water they would need from the rain! They used rain catchments to get the water and a whole bunch of big tanks to hold it!

We can use so simple multiplication to find out how much water they would need to collect. First we need some givens, or facts that we can work off of.

Givens:
The average person needs about 4 litres of water a day to wash, drink and cook with.
The mission, while still using the rain catchments, had about 20 people in all using the supply.
The dry season would last about 6 months a year on average (Sometimes it would be more, and sometimes less, but we will go with 6 months as an average).

The Math:
The amount of water a person uses in 6 months can be found by multiplying first by 7 (the number of days in week), then by 4 (4 weeks in a month), then by 6 (6 months in the dry season).

4 x 7 x 4 x 6 = 672

A person would use 672 litres in 6 months! That’s crazy!

How many litres would 20 people use in 6 months?

672 x 20 = 13, 440

20 people would use 13, 440 litres in 6 months! Wow!

With this number in their mind, the missionaries could find out what quantity of water their water tanks would hold.

As the mission got bigger and swelled with an overwhelming amount of people, they had to put in a pipeline from a spring about 8 kilometres away!

Suggested activities:

If you and a about 15 other mates, or friends were going to go and set up a community in the middle of nowhere, could you find out how much water you would need to have available?
Think about how long at a time that it wouldn’t rain for.
How much water would you use in a day?
Also, would you ever wash up?…

By,
Crister

2001 September 17. Monday. North of Ace Bore.

The heart of the fire we saw today was basically a bare piece of black and red ground. The action was at the edges of a circle surrounding this. The burning area itself was but a yard or two in width, and travelling gradually outward. I skipped through the ‘frontier’ of the burning, onto the blackened ground, and felt the heat of the sand – it was very similar to the temperature of the sand we had sat upon at billy tea break. This means the fire must be travelling quickly, to not have time to heat the ground as it passes across it.

Although a light but steady wind was present, it did little to blow the fire in any particular direction, so that the only things keeping it from burning outward in a geometric circle were fire-breaks such as the track we followed, and variation in the make up of the groundcover - especially underneath desert oaks, the tallest trees to be found in this area. At some points, the fire did manage to cross the track, as it is rarely used and very overgrown. Here we saw an hourglass shape as the burning ‘funneled’ through the gap.

If a fire began in an evenly vegetated area, where there was no road to distort it, and burned out a circle, we could calculate the area which would be burnt after a given amount of time, by observing how fast the fire travels, and using the formula for the area of a circle: πR2, where R is the radius, or half of the distance across the circle.
If a fire circle with a diameter of eighteen metres travelled at six metres per minute in every direction, work out the following:

* The area of the initial burnt section
* How large the circumference – distance around the fire - would be.
* The diameter of the fire circle after five minutes burning.
* The area of the circle after five, fifteen, and thirty minutes burning.
* How long would it take for the fire to cover one square kilometre.

The bushfires here can be pretty frightening. As I write this, I can see one glowing in the night sky behind me, not too far from camp. In order to get my mind off it, I’ve come up with this little math problem for you to puzzle over:

Bushfires often start in one location and spread outward in a widening circle. The flames can spread with the wind at a speed of up to 50 kilometers per hour!

a) If the distance from the center of the fire to it edge is 200 meters, what circular area has the fire covered?
b) If the fire spreads out from the center as fast as possible (50 kph), how long will it take for the fire to cover a circular area of 100 kilometers?

Have you ever thought how something as benign as a rabbit could become such an ecological nightmare? Let’s take a look at how their patterns of development became such an environmental problem in the Australian Outback.

Rabbits live in underground burrows among dense vegetation, which also provides their food source. They are well protected from predators in these burrows as they can quickly hide.

A female rabbit may have up to five litters of five to seven offspring per year. Although the life span of a rabbit in the wild is not lengthy (maybe two to five years), she is able to reproduce by six months of age. (And, remember, this is only ONE rabbit!)

In a good year, with limited predators (dingoes, foxes, cats), rabbits may reproduce by the thousands. In the Tanami Desert region, with limited vegetation in a normal year, native species of herbivores, like the Bilby, will starve.

Suggested activities: How many offspring can one female rabbit have in her lifetime? Compute the number of rabbits born per year per female rabbit. Imagine the total number of offspring produced per year by a rabbit population if there are 100 rabbits living within a one square kilometre area. If the square kilometre can support only 100 rabbits, what will be the effect of a growing rabbit population on the surrounding area?

April

Download today's lesson activity (PDF)

THEME: Road to Lajamanu
SUBJECT: Maths

This unusual marker we came across 40 kms outside Lajamanu is known as a trig, or Trigonometry Point. They are built on the most prominent geological formation in the surrounding countryside so they can be seen from long distances. By sighting two or more Trig Points and taking a compass bearing allows surveyors to accurately determine their position on a map when plotting boundary lines of property, etc.

Note the two bisecting square sheets of iron on the top of the pole. This ensures that the full size will be seen from any angle. Lasers are also used with these trig points to accurately determine the distance the trig point is from your position.

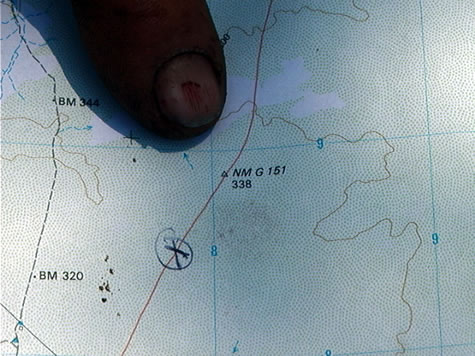
For example:
The surveyor can see trig point A and Trig Point B from the homestead. From the map the surveyor knows that the distance between Trig A and Trig B is 12 kilometres. The angle between the compass bearings of A and B is 105 degrees. What is the distance from the homestead to Trig Point A?

Suggested actives:

Can you find any geological landmarks in your area? If so, does a map say the distance between them? Can you use trigonometry to find the distance from your house to one point?

By, Bushman John and his apprentice Crister